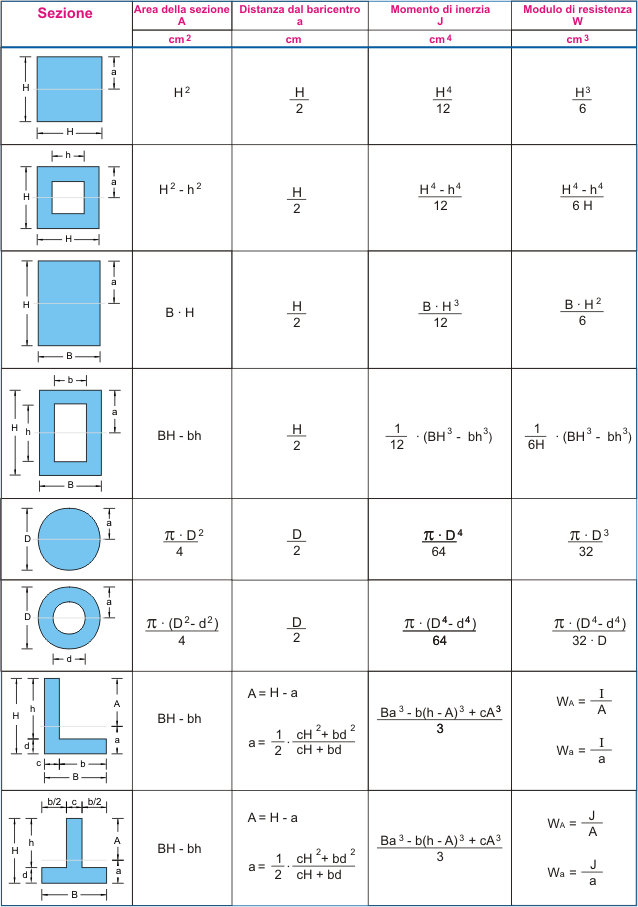
Esempio 1: calcolo di una trave in legno
Immaginiamo una trave di lunghezza L appoggiata sulle due estremità, con una forza F applicata al centro.
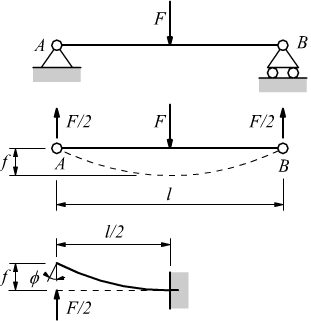
La trave è in equilibrio statico (non trasla e non ruota), quindi la somma delle forze e la somma dei momenti è uguale a zero. La reazione vincolare degli appoggi A e B vale F/2, perchè la forza F è applicata al centro. La somma algebrica delle forze (tutte verticali in questo caso) vale zero.
Scegliamo come punto per il calcolo dei momenti il punto di applicazione della forza F, per comodità, e calcoliamo il momento di ciascuna forza rispetto a questo punto. Il momento generato dalla reazione vincolare nel punto A ha segno orario e vale F/2*L/2. Il momento generato dalla reazione vincolare B vale -F/2*L/2. I due momenti sono uguali e di segno opposto, quindi la somma è zero e la condizioni di non-rotazione è soddisfatta. Il momento massimo è al centro della trave e vale F/2*L/2.
Mmax=F*L/4=800 *3000 /4= 600.000 Nmm
Ipotizziamo che la trave sia di legno (sigma = 30 N/mm2), di sezione 10×10 cm.
Il modulo di resistenza vale: H^3/6= 100^3 /6 = 1666,6 mm3
Lo sforzo nel materiale (sigma, N/mm2) vale:
sigma=Mmax/W =600.0002400 * 10^3 / 416,6 = 5761 N/mm2
Esempio 2: calcolo di una piastra di sollevamento in acciaio (bilancino)
Una piastra d’acciaio S355 di lunghezza L=700 mm, altezza H=150 mm e spessore B=16 mm è parte di un meccanismo di sollevamento di una turbina eolica. Il peso della turbina eolica é applicato alle estremitá, mentre il bozzello della gru é collegato al centro della piastra.
Si vuole conoscere la portata della piastra.
Il modulo di resistenza vale: W = (B*H^3) /6 = 16*150^3/6 = 9 * 10^6 mm3
Mmax = sigma*W = 355*9.000.000 =3,195 *10^6 Nmm
Mmax=F*L/4
F=Mmax*4/L= 3,195 *10^6 *4 /700=18,26 kN
F=18,26*9,81=179 ton
Esempio 3 – Calcolo di una mensola in acciaio
Una mensola di una passerella pedonale é realizzata mediante elementi 70×70 cm in pianta in lamiera di alluminio. Sotto la lamiera vi sono due elementi in ferro piatto 10×50 mm murati nella parete rocciosa. Il lato lungo é verticale La mensola sporge 70 cm. Calcolare la porta della mensola a snervamento del ferro piatto in S235.
Il modulo di resistenza vale:
W = (B*H^3) /6 =5*10^2/6=4167 mm3
Il momento massimo vale:
M=W*sigma= 4167 * 235 = 979167 Nmm =979 Nm
Il braccio é 0,7 m quindi la forza massima in punta per un elemento é:
F= M/b= 979/0,7 = 1399 Nm = 142 kg
La portata della mensola in punta é il doppio: 184 kg